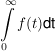KonvergenzkriteriumSätze Konvergenzkriterien für Reihen
Universität
Satz (Leibniz-Kriterium) Sei 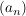 eine monoton fallende Nullfolge reeller Zahlen. eine monoton fallende Nullfolge reeller Zahlen.
Dann ist die alternierende Reihe 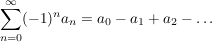 konvergent, und für ihre Summe gilt konvergent, und für ihre Summe gilt
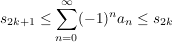 ,
wobei 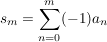 , die m-te Partialsumme ist. , die m-te Partialsumme ist.
Insbesondere gilt die Fehlerabschätzung
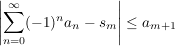 .
Quelle: (1)
Quelle: (1)
Satz (Majorantenkriterium) Es seien 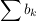 eine konvergente Reihe reeller Zahlen 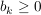 und 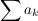 eine Reihe komplexer Zahlen.
Gilt 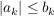 für alle 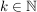 , so konvergiert auch 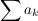 , und zwar sogar absolut. Es gilt 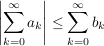 .
Quelle: (1)
Satz (Quotientenkriterium) Es sei 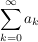 eine Reihe komplexer Zahlen mit 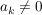 für fast alle 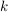 . Ferner gebe es eine reelle Zahl 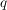 mit 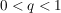 und 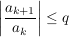 für fast alle 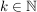 .
Dann ist die Reihe 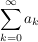 absolut konvergent.
Insbesondere konvergiert 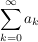 absolut, wenn die Folge der Quotienten 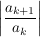 gegen eine Zahl 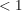 konvergiert.
Quelle: (1)
Satz (Wurzelkriterium) Es sei 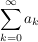 eine Reihe komplexer Zahlen.
Gilt ![$ \limsup_{n\to\infty} \wurzel[n]{|a_n|} < 1 $ $ \limsup_{n\to\infty} \wurzel[n]{|a_n|} < 1 $](/teximg/7/1/01797017.png) oder ![$ \wurzel[n]{|a_n|}< q $ $ \wurzel[n]{|a_n|}< q $](/teximg/8/0/01343808.png) für eine positive Zahl 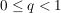 für fast alle Indizes 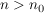 , so konvergiert die Reihe 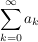 und zwar sogar absolut.
Gilt ![$ \wurzel[n]{|a_n|}\ge 1 $ $ \wurzel[n]{|a_n|}\ge 1 $](/teximg/0/1/01343810.png) für unendlich viele  , so ist die Reihe 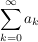 divergent.
Quelle: (2)
Quelle: (1)
Quelle: (1)
Quelle: (1)
Quelle: (1)
Satz (Integralkriterium für Reihen) Sei 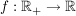 eine monotone und stetige Funktion.
Genau dann konvergiert die Reihe 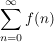 , wenn das Integral 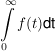 konvergiert.
Quelle: (1)
Quellen
(1) isbn3411032049
(2) Mathe-Online-Lexikon
Bemerkungen.
Weitere Bemerkungen zum Verständnis des Satzes.
Beispiele.
Beweis.
|