Diophantische GleichungWenn man sich bei einer Gleichung nur für Lösungen interessiert, die ganzzahlig
sein sollen, spricht man von einer diophantischen Gleichung, nach dem griechischen
Mathematiker Diophantos von Alexandrien .
Wikipedia-Artikel: Diophantische Gleichung .
Die Bedingung der Ganzzahligkeit der Lösungen hat zur Folge, dass für diophantische
Gleichungen im Allgemeinen ganz andere Lösungsmethoden zum Zug kommen als für
"gewöhnliche" Gleichungen ohne diese Einschränkung. Die Theorie der diophantischen
Gleichungen ist deshalb ein Zweig der Zahlentheorie , in welcher man sich mit den
Eigenschaften der ganzen Zahlen beschäftigt.
Es gibt eine Reihe sehr berühmter und wichtiger diophantischen Gleichungen, darunter
zum Beispiel die Gleichung
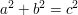
für ganzzahlige Seitenlängen eines rechtwinkligen Dreiecks (pythagoräische Tripel),
die Gleichung des "Großen Satzes von Fermat", welcher besagt, dass
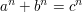
für ganze Zahlen 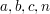 mit mit 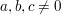 und und 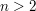 keine Lösungen besitzt. keine Lösungen besitzt.
Dieser Satz - zuerst wohl nicht viel mehr als eine (allerdings gute) Vermutung -
musste allerdings 357 Jahre lang auf seinen endgültigen Beweis warten.
Eine wichtige Rolle spielen auch die linearen diophantischen Gleichungen
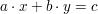
(mit vorgegebenen Werten von 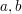 und und  ) )
sowie die "Pellsche Gleichung"
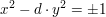 (mit (mit 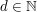 ) )
Beispiele:
Wir betrachten hier nur zwei Beispiele, um einen kleinen Einblick in die Methode der
Behandlung solcher Gleichungen zu geben.
Beispiel 1: eine lineare diophantische Gleichung
Für welche natürlichen Zahlen x und y gilt die Gleichung
18 x + 57 y = 1000 ?
Man kann sich leicht davon überzeugen, dass diese Gleichung keine ganzzahligen
Lösungen haben kann, denn die linke Seite ist durch 3 teilbar, die rechte aber nicht.
Ändern wir also die rechte Seite zu 1200 ab:
18 x + 57 y = 1200
Diese Gleichung können wir jetzt natürlich durch 3 teilen:
6 x + 19 y = 400 (G)
Nun betrachten wir zunächst die entsprechende homogene Gleichung, welche rechts
eine Null stehen hat:
6 x + 19 y = 0 (H)
Der Überblick über die Lösungen dieser homogenen Gleichung ist leicht zu gewinnen.
Wir nehmen für x ein Vielfaches von 19 und für y das entsprechende Vielfache von 6,
aber mit entgegengesetztem Vorzeichen:
x = 19 t y = -6 t (t 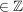 ) )
oder als Paar zusammengefasst:
(x,y) (t) = (19t , -6t)
Damit (und auf keine andere Weise) wird (H) erfüllt.
Zweitens betrachten wir die Gleichung
6 x + 19 y = 1 (P)
bei welcher rechts eine Eins steht (allenfalls der ggT der Faktoren, welche vor x und y
stehen - in unserem Beispiel ist ggT(6,19) = 1 ).
Von dieser Gleichung brauchen wir nur ein einziges spezielles Lösungspaar.
Für jeden, der das Kopfrechnen noch nicht total verlernt hat, ist offensichtlich,
dass das Paar (x,y) = (-3,1) diese Gleichung erfüllt.
Multiplizieren wir dieses Paar mit dem Faktor 400 (rechte Seite von G), haben wir
natürlich wegen der Linearität der Gleichung ein "partikuläres" Lösungspaar von (G) :
400  (-3 , 1) = (-1200 , 400) (-3 , 1) = (-1200 , 400)
Nun kann man einfach diese spezielle Lösung der Gleichung (G) zur allgemeinen
Lösung von (H) addieren und erhält damit eine Formel zur Berechnung der
"allgemeinen", mit anderen Worten jeder beliebigen Lösung der Gleichung (G):
(x,y) = (19t , -6t) + (-1200,400) = (19t-1200 , 400-6t)
Diese Formel ergäbe mit 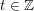 unendlich viele Lösungspaare. Da wir aber nur unendlich viele Lösungspaare. Da wir aber nur
solche mit natürlichen, also positiven x und y wollten, ergibt sich aus x=19t-1200>0
und y=400-6t>0, dass nur die Werte t=64, t=65, t=66 in Frage kommen. Das
führt auf die drei Lösungspaare
(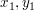 ) = (16,16) ) = (16,16)
(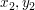 ) = (35,10) ) = (35,10)
(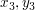 ) = (54,4) ) = (54,4)
Beispiel 2: eine unlösbare Gleichung
Wenn wir in der oben genannten "Pythagorasgleichung", welche unendlich viele
Lösungstripel 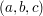 hat, auf der rechten Seite einen Faktor 3 dazusetzen, erhal- hat, auf der rechten Seite einen Faktor 3 dazusetzen, erhal-
ten wir die Gleichung
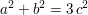
Diese neue Gleichung hat aber überhaupt kein ganzzahliges Lösungstripel ausser dem
trivialen 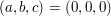 . Dies soll bewiesen werden. Der Beweis erfolgt nach dem . Dies soll bewiesen werden. Der Beweis erfolgt nach dem
Schema des "Beweises durch Widerspruch". Wir nehmen also an, wir hätten ein Tripel
(a,b,c) von 3 ganzen Zahlen, nicht alle gleich Null, welche die Gleichung erfüllen, und
zeigen dann, dass diese Annahme auf einen Widerspruch führt.
Nebst der Voraussetzung 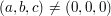 dürfen wir annehmen, dass keine der dürfen wir annehmen, dass keine der
drei Zahlen negativ sein soll (andernfalls wechseln wir ihr Vorzeichen, was an der Gültig-
keit der Gleichung nichts ändert). Ferner dürfen wir annehmen, dass nicht alle drei Zahlen
gerade seien. Wäre dies der Fall, so könnten wir alle drei Zahlen halbieren und hätten damit
ein neues Tripel, welches die Gleichung ebenfalls erfüllt. Es soll also solange gekürzt werden,
bis noch höchstens 2 der Zahlen 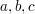 gerade sind. Für die Belegung von gerade sind. Für die Belegung von 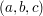 mit geraden mit geraden
(g) oder ungeraden (u) Werten gibt es also nur noch folgende Möglichkeiten:
1.) (u,u,u)
2.) (u,u,g)
3.) (u,g,u)
4.) (u,g,g)
5.) (g,u,u)
6.) (g,u,g)
7.) (g,g,u)
Die Möglichkeiten 1.), 4.), 6.), 7.) fallen aber sofort ebenfalls weg, weil bei allen diesen auf
den beiden Seiten der Gleichung 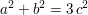 Werte unterschiedlicher Parität entstehen Werte unterschiedlicher Parität entstehen
würden. Ferner sind die Möglichkeiten 3.) und 5.) analog (Vertauschung von a und b, was
unerheblich ist). Zu untersuchen bleiben also die Fälle 2.) und 3.) .
Für das Folgende betrachten wir nun die Zahlen 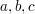 modulo 4. Beim Rechnen modulo 4 modulo 4. Beim Rechnen modulo 4
in der Menge 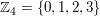 gilt gilt 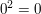 und und 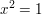 für alle für alle 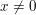 . Insbesondere ist . Insbesondere ist
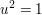 für alle ungeraden für alle ungeraden  . Für geradzahlige Werte . Für geradzahlige Werte 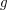 gilt entweder gilt entweder 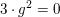 ( falls ( falls 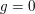 ) )
oder aber 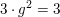 ( falls ( falls 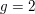 ) . ) .
Im Fall 2.) würde nun also aus 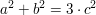 modulo 4 folgen, dass modulo 4 folgen, dass 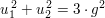 , ,
was unmöglich ist, weil 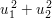 stets stets 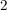 ergibt, ergibt, 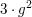 aber entweder aber entweder 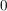 oder oder 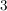 . .
Im Fall 3.) hätten wir analog (modulo 4) die Gleichung 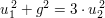 . Dies würde entweder . Dies würde entweder
auf 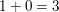 oder auf oder auf 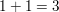 führen, was beides falsch ist. führen, was beides falsch ist.
Da also alle grundsätzlich möglichen Belegungen von 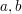 und und  mit Werten beliebigen Rests mit Werten beliebigen Rests
modulo 4 mit der Gleichung 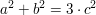 unvereinbar sind, ist bewiesen: unvereinbar sind, ist bewiesen:
Diese diophantische Gleichung hat kein nicht-triviales Lösungstripel. 
Eine Folgerung aus diesem Ergebnis ist z.B. die Erkenntnis, dass es in der Ebene 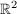
Kreise gibt ( etwa 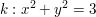 ), welche keinen einzigen Punkt ), welche keinen einzigen Punkt 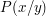 mit rationalen mit rationalen
x und y enthalten.
| 